저번 포스팅에서는 θ0 = 0인 경우에 해당하는 Cost Function에 대해 알아보았는데, 이번 포스팅에서는 θ0가 0이 아닌 경우에 대해 알아보자. (이번에도 Coursera 강의를 참고하여 포스팅합니다.)
먼저 Cost Function에 대해서 다시 보면

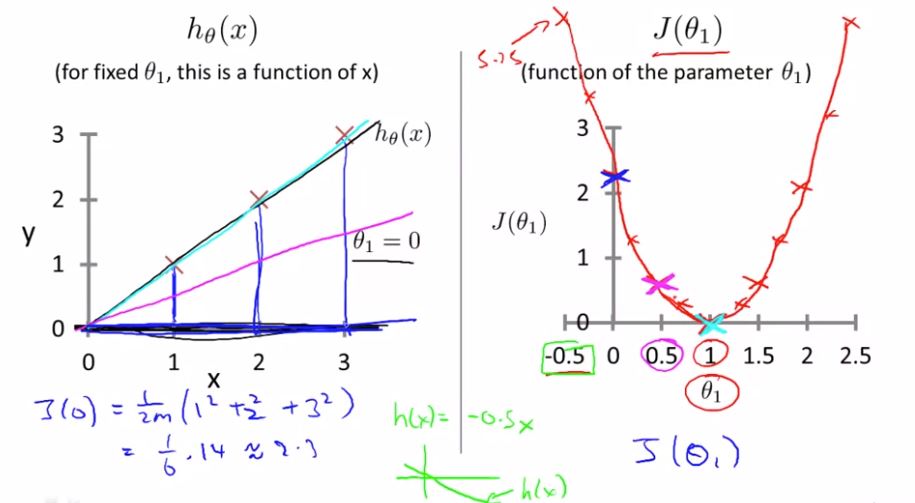
이렇게 정리할 수 있다. 여기서 생각해야 할 것은 위의 Hypothesis에도 나와있지만 우리는 선형 회귀일 때의 Cost Function을 구하고 있다는 것이다. 저번 포스팅의 경우 역시 선형 회귀인 경우이고 θ0 = 0였기 때문에 Cost Function은 J(θ1)과 θ1, 즉, 변수가 2개이므로 아래 그림처럼 2차원 형태였다.
하지만, θ0가 0이 아닌 경우는 θ0가 살아있기 때문에 J(θ0, θ1)과 θ1, θ0, 즉, 변수가 3개이므로 Cost Function이 3차원 형태를 띄게 된다.

그림에서도 보이듯이 3차원 모양의 활 형태를 띄고 있다. 선형 회귀에서는 이렇게 활모양이지만 선형 회귀가 아닌 경우에는 활 모양이 아닐 수도 있다는 점을 생각하자. 다시 돌아와서, 이 활 모양을 다른 각도에서 보게 되면

이전 그림이 약간 위에서 본 것이라면 위 그림은 약간 아래에서 본 것이다. θ1, θ0이 바닥에 깔려있어 약간 겹치듯이 보인다. 위 그림의 위쪽을 잘 보면, 활 모형이 있는 공간이 정육면체 모형임을 알 수 있다(즉, 3차원). 이 활 형태의 모형이 바로 θ0 != 0일 때(!은 NOT)의 Cost Function이다.
이 모형을 잘 보면 J(θ0, θ1)축이 Cost Function값이므로 J(θ0, θ1)축이 가장 낮은 지점이 Cost Function의 최소값이 된다는 사실을 알 수 있다. 하지만, 이 점들은 3차원이기 때문에 표현하기가 쉽지가 않으므로 우리는 이를 정사영시켜 한 차원 낮춘 2차원 형태로 표현한다.

실제로 보면 x,y축이 θ0,θ1축인 것을 확인할 수 있고 모양이 등고선 형태로 나오게 되는데, 이렇게 둥그런 모양끼리는 모두 Cost Function값, 즉, J(θ0, θ1)이 같다. 하나의 예로, 위의 연두색에 있는 모든 점들끼리는 Cost Function값이 같다.
그럼 이 등고선 그래프에서 Cost Function의 최소값은 어디일까? 정사영을 시켰다는 사실에 기반한다면 가장 안쪽에 있는 원 방향 (이 포스팅에서는 가운데 방향으로 칭하겠습니다) 임을 유추해볼 수 있다. 잘 모르겠으면 아까 위에서 봤던 활 모형을 떠올려보고 이를 위에서 본다고 생각해보자. (이게 정사영 개념)
저번 포스팅에서 Cost Function을 보고 h(x)를 그렸듯이 이번에도 똑같이 해보자.

오른쪽 그래프에서 빨간색으로 X 표시된 부분이 (θ0, θ1) = (800, -0.15)이다. 즉, h(x) = -0.15x + 800이다. 그래서, 왼쪽 그래프처럼 그려진 것이다. 오른쪽 그래프를 보면, 빨간색으로 X 표시된 부분이 가운데 빨간 점(Cost Function 최소값)과 어느 정도 떨어져 있다는 점과 왼쪽 그래프(직선)를 봤을 때 데이터의 분포와 거의 비슷하지 않고 그래프 바깥의 점들과 그래프의 거리가 많이 먼 것으로 보아 좋은 가설(h(x)) (또는 모델)은 아닌 것을 알 수 있다. 다른 지점도 살펴보자.

오른쪽 그래프에서 빨간색으로 X 표시된 부분이 (θ0, θ1) = (360, 0)이다. 즉, h(x) = 0*x + 360이다. 그래서, 왼쪽 그래프처럼 그려진 것이다. 오른쪽 그래프를 보면, 빨간색으로 X 표시된 부분이 가운데 빨간 점(Cost Function의 최소값)과 이전보단 가까워졌지만 여전히 어느 정도 떨어져 있다는 점과 왼쪽 그래프를 봤을 때 이전 그래프보단 데이터의 분포가 그래프와 더 많이 일치하지만 그래프 바깥의 점들과 그래프의 거리가 꽤 있는 것으로 보아 이 역시 좋은 가설(h(x))은 아닌 것을 알 수 있다. 그럼 이번엔 Cost Function의 최소값이 있는 가운데인 경우를 보자.

오른쪽 그래프에서 빨간색으로 표시된 부분이 (θ0, θ1) = (220, 0.12)이다. 즉, h(x) = 0.12x + 220이므로 왼쪽 그래프처럼 그려진 것이다. 오른쪽 그래프를 보면, 빨간색으로 표시된 부분이 가운데에 위치하고 있고 왼쪽 그래프를 봤을 때 이전 그래프들보단 데이터의 분포가 그래프와 더 많이 일치하고 그래프 바깥의 점들과 그래프와의 거리도 그리 멀지 않다.
물론 이 가설(h(x)) 역시 모든 데이터들을 만족시키지는 못한다. 이 경우가 Cost Function의 최소값인 즉, 해당 데이터에 가장 맞는 가설(또는 모델)인 것이다.
이렇게 데이터들이 다양하게 분포해있기 때문에 이를 완전히 만족하는 선형그래프는 거의 찾을 수 없다. 이 얘기는 Cost Function이 0인 값을 찾기는 쉽지 않다는 뜻이다. 그래서, 해당 데이터들의 조건에 맞는 Cost Function을 찾되 0인 경우를 찾는다고 하지 않고 최소값을 찾는다고 하는 것이다. Cost Function이 최소값일 때의 가설 H(x)가 그나마 해당 데이터들의 분포와 가장 비슷하다고 할 수 있다.
참고 사이트 :
'Machine Learning' 카테고리의 다른 글
| Multiple Features in Linear Regression (= Multivariate linear regression(다변량 선형회귀)) (0) | 2020.08.11 |
|---|---|
| Gradient Descent (경사하강법) (2) (feat. Learning rate) (0) | 2020.07.31 |
| Gradient Descent (경사하강법) (1) (0) | 2020.07.16 |
| Cost Function (비용 함수) (1) (0) | 2020.06.12 |
| Linear Regression (선형 회귀) (Feat. Cost Function) (0) | 2020.06.11 |



댓글